Векторы — это фундаментальное математическое понятие, позволяющее описать направление и величину. В играх и приложениях векторы часто используются для описания некоторых фундаментальных свойств, таких как положение персонажа, скорость движения или расстояние между двумя объектами.
Векторная арифметика имеет фундаментальное значение для многих аспектов компьютерного программирования, таких как графика, физика и анимация, и полезно глубоко разобраться в ней, чтобы получить максимальную отдачу от Unity.
Векторы могут быть выражены в нескольких измерениях, и Unity предоставляет классы Vector2, Vector3 и Vector4 для работы с 2D-, 3D- и 4D-векторами. Все эти три типа классов векторов имеют много общих функций, таких как величина, поэтому большая часть информации на этой странице относится ко всем трем типам векторов, если не указано иное.
На этой странице представлен обзор классов Vector и их общего использования при написании сценариев с ними. Исчерпывающую информацию о каждом члене векторных классов см. на справочных страницах скриптов для Vector2, Вектор3 и Вектор4.
Знакомство с векторной арифметикой
Дополнение
При сложении двух векторов результат эквивалентен взятию исходных векторов в качестве «шагов» один за другим. Обратите внимание, что порядок двух параметров не имеет значения, так как результат будет одинаковым в любом случае.
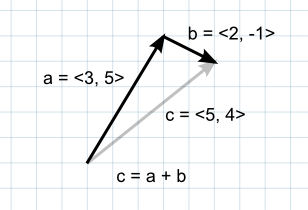
Если первый вектор принять за точку в пространстве, то второй можно интерпретировать как смещение или «скачок» от этой позиции. Например, чтобы найти точку на 5 единиц выше точки на земле, вы можете использовать следующий расчет:-
var pointInAir = pointOnGround + new Vector2(0, 5);
Если векторы представляют собой силы, то более интуитивно понятно думать о них с точки зрения их направления и величины (величина указывает на размер силы). Добавление двух векторов сил приводит к новому вектору, эквивалентному комбинации сил. Эта концепция часто полезна при приложении сил с несколькими отдельными компонентами, действующими одновременно (например, ракета, движущаяся вперед, также может подвергаться воздействию бокового ветра).
Хотя в приведенных здесь примерах показаны двумерные векторы, одна и та же концепция применима к трехмерным и четырехмерным векторам.
Вычитание
Вычитание векторов чаще всего используется для определения направления и расстояния от одного объекта до другого. Обратите внимание, что порядок двух параметров действительно имеет значение при вычитании:-
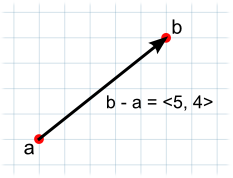
// The vector d has the same magnitude as c but points in the opposite direction.
var c = b - a;
var d = a - b;
Как и в случае с числами, сложение отрицательного значения вектора равносильно вычитанию положительного числа.
// These both give the same result.
var c = a - b;
var c = a + -b;
Отрицательное значение вектора имеет ту же величину, что и оригинал, и указывает на ту же прямую, но в совершенно противоположном направлении.
Направление и расстояние от одного объекта до другого
Если одну точку в пространстве вычесть из другой, то в результате получится вектор, который «указывает» от одного объекта к другому:
// Gets a vector that points from the player's position to the target's.
var heading = target.position - player.position;
Помимо того, что этот вектор указывает в направлении целевого объекта, величина этого вектора равна расстоянию между двумя позициями. Вам может понадобиться «нормализованный» вектор, указывающий направление на цель, но с фиксированным расстоянием (скажем, для направления снаряда). Вы можете нормализовать вектор, разделив его на собственную величину:
var distance = heading.magnitude;
var direction = heading / distance; // This is now the normalized direction.
Этот подход предпочтительнее, чем отдельное использование как величины, так и нормализованных свойств, так как оба они довольно требовательны к процессору (оба требуют вычисления квадратного корня).
Если вам нужно использовать только расстояние для сравнения (скажем, для проверки близости), вы можете вообще не вычислять величину. Свойство sqrMagnitude дает квадрат значения величины и вычисляется как величина, но без трудоемкой операции извлечения квадратного корня. Вместо того, чтобы сравнивать величину с известным расстоянием, вы можете сравнить квадрат величины с квадратом расстояния:-
if (heading.sqrMagnitude < maxRange * maxRange) {
// Target is within range.
}
Это намного эффективнее, чем использование истинной величины при сравнении.
Иногда при работе в 3D может потребоваться "надземный курс" к цели. Например, представьте игрока, стоящего на земле, которому нужно приблизиться к парящей в воздухе цели. Если вычесть положение игрока из положения цели, то результирующий вектор будет направлен вверх к цели. Это не подходит для ориентации преобразования игрока, поскольку они также будут указывать вверх; что действительно необходимо, так это вектор от положения игрока к положению на земле прямо под целью. Вы можете получить это, взяв результат вычитания и установив координату Y равной нулю:-
var heading = target.position - player.position;
heading.y = 0; // This is the overground heading.
Scalar Multiplication and Division
При обсуждении векторов обычное число (например, значение с плавающей запятой) называют скаляром. Смысл этого в том, что у скаляра есть только «масштаб» или величина, тогда как у вектора есть и величина, и направление.
Умножение вектора на скаляр приводит к тому, что вектор указывает в том же направлении, что и исходный. Однако величина нового вектора равна исходной величине, умноженной на скалярное значение.
Аналогично скалярное деление делит величину исходного вектора на скаляр.
Эти операции полезны, когда вектор представляет смещение движения или силу. Они позволяют изменять величину вектора, не влияя на его направление.
Когда любой вектор делится на его собственную величину, результатом является вектор с величиной 1, который известен как нормализованный вектор. Если нормализованный вектор умножается на скаляр, то величина результата будет равна этому скалярному значению. Это полезно, когда направление силы постоянно, но сила управляема (например, сила от колеса автомобиля всегда толкает вперед, но мощность контролируется водителем).
Дополнительный продукт
Скалярное произведение берет два вектора и возвращает скаляр. Этот скаляр равен сумме двух векторов, умноженных вместе, и результату, умноженному на косинус угла между векторами. Когда оба вектора нормализованы, косинус по существу определяет, насколько первый вектор простирается в направлении второго (или наоборот — порядок параметров не имеет значения).
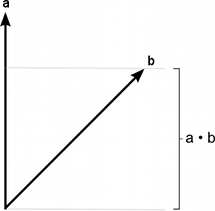
Ниже вы можете увидеть сравнение того, как векторы с разными углами по сравнению с эталонным вектором возвращают значение скалярного произведения между 1 и –1:
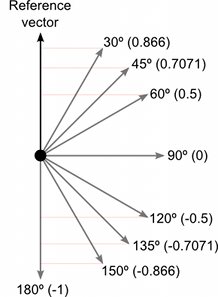
Скалярное произведение – это математически более простая операция, чем вычисление косинуса, поэтому в некоторых случаях ее можно использовать вместо функции Mathf.Cos или операции векторной величины (оно не делает то же самое, но иногда эффект равнозначный). Однако вычисление функции скалярного произведения требует гораздо меньше процессорного времени, поэтому его можно оптимизировать.
Скалярное произведение полезно, если вы хотите вычислить величину величины одного вектора, лежащую в направлении другого вектора.
Например, автомобильный спидометр обычно измеряет скорость вращения колес. Автомобиль может двигаться не прямо вперед (например, он может скользить вбок), и в этом случае часть движения будет не в том направлении, в котором машина смотрит, и поэтому не будет измеряться спидометром. Величина жесткого телакомпонента объекта, позволяющего воздействовать на GameObject смоделированной гравитацией и другими силами. Подробнее
См. в Словарь. Вектор скорости даст скорость в направлении общего движения но чтобы изолировать скорость в прямом направлении, вы должны использовать скалярное произведение:
var fwdSpeed = Vector3.Dot(rigidbody.velocity, transform.forward);
Естественно, направление может быть любым, но для этого расчета вектор направления всегда должен быть нормализован. Мало того, что результат является более правильным, чем величина скорости, он также позволяет избежать медленной операции извлечения квадратного корня, связанной с нахождением величины.
Перекрестный продукт
Перекрестное произведение имеет смысл только для трехмерных векторов. Он принимает два трехмерных вектора в качестве входных данных и возвращает другой трехмерный вектор в качестве результата.
Вектор результата перпендикулярен двум входным векторам. Вы можете использовать «правило правого винта», чтобы запомнить направление выходного вектора из порядка входных векторов. Если вы можете согнуть пальцы в порядке входных векторов, ваш большой палец будет указывать в направлении выходного вектора. Если порядок параметров изменить на противоположный, результирующий вектор будет указывать в прямо противоположном направлении, но будет иметь ту же величину.
Величина результата равна сумме входных векторов, умноженных вместе, а затем полученному значению, умноженному на синус угла между ними. Некоторые полезные значения функции синуса показаны ниже:-
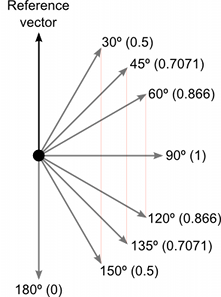
Перекрестное произведение может показаться сложным, поскольку в возвращаемом значении оно объединяет несколько полезных фрагментов информации. Однако, как и скалярное произведение, оно очень эффективно с математической точки зрения и может использоваться для оптимизации кода, который в противном случае зависел бы от более медленных трансцендентных функций, таких как синус и косинус.
Вычисление нормального/перпендикулярного вектора
«Нормальный» вектор (т. е. вектор, перпендикулярный плоскости) часто требуется в meshосновном графическом примитиве Единства. Меши составляют большую часть ваших 3D-миров. Unity поддерживает триангулированные или четырехугольные полигональные сетки. Поверхности Nurbs, Nurms, Subdiv должны быть преобразованы в полигоны. Подробнее
См. при генерации Словарь, а также полезен при следовании по пути и в других ситуациях. Учитывая три точки на плоскости, скажем, угловые точки треугольника сетки, вы можете найти нормаль следующим образом:
- Выберите один из трех пунктов
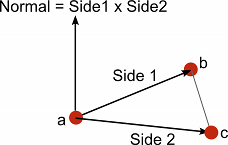
- Вычтите его из каждой из двух других точек отдельно (в результате получится два новых вектора: «Сторона 1» и «Сторона 2»).
- Вычислить векторное произведение векторов «Сторона 1» и «Сторона 2»
- Результатом перекрестного произведения является новый вектор, который перпендикулярен плоскости, на которой лежат три исходные точки - "нормаль".
Vector3 a;
Vector3 b;
Vector3 c;
Vector3 side1 = b - a;
Vector3 side2 = c - a;
Vector3 normal = Vector3.Cross(side1, side2);
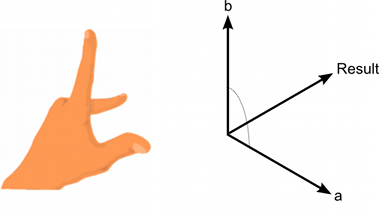
"Правило левой руки" можно использовать для определения порядка, в котором два вектора должны быть переданы в функцию векторного произведения. Когда вы смотрите вниз на верхнюю сторону поверхности (от которой нормаль будет направлена наружу), первый вектор должен перемещаться по часовой стрелке ко второму:
Результат будет указывать точно в противоположном направлении, если порядок входных векторов обратный.
Для сеток вектор нормали также должен быть нормализован. Это можно сделать с помощью свойства normalized, но есть еще один трюк, который иногда бывает полезен. Вы также можете нормализовать перпендикулярный вектор, разделив его на его величину:-
float perpLength = perp.magnitude;
perp /= perpLength;
Еще одно полезное замечание: площадь треугольника равна perpLength / 2. Это полезно, если вам нужно найти площадь поверхности всей сетки или вы хотите выбрать треугольники случайным образом с вероятностью, основанной на их относительных площадях.


